Pengertian Permutasi, Kombinasi, dan Perbedaannya

Sebelumya, sobat idschool sudah mempelajari tentang aturan pengisian tempat tang merupakan bagian dari materi peluang. Materi peluang lainnya yang akan dibahas kali ini adalah tentang permutasi, kombinasi, dan perbedannya.

Permutasi membahas tentang penyusunan k objek dari n objek yang tersedia dengan memperhatikan urutannya. Kombinasi berguna untuk menentukan penyusunan k objek dari n objek yang tersedia tanpa memperhatikan urutannya. Pada bagian akhir, sobat idschool akan dijelaskan mengenai contoh-contoh permasalahan terkait permutasi atau kombinasi. influencer marketing jakarta juga merupakan strategi dalam memasarkan sebuah produk

 Selain itu, akan diberikan contoh soal beserta pembahasannya untuk memperdalam pehaman sobat idschool tentang materi permutasi, kombinasi, dan perbedaanya. Jadi, simak materi yang akan diberikan sampai akhir.

Permutasi

     Materi pertama yang akan dibahas pada permutasi, kombinasi, dan perbedaannya adalah permutas. Permutasi mempelajari tentang menyusun k objek dari n objek dengan memperhatikan urutan. Terdapat tiga contoh permutasi yang sering muncul yaitu permutasi dari unsur-unsur yang berbeda, permutasi dengan beberapa unsur yang sama, dan permutasi siklik. Simak penjabaran lebih lanjut pada penjabaran di bawah.

Macam-macam permutasi:

1. Permutasi dari unsur-unsur yang berbeda yaitu banyaknya cara untuk menyusun k unsur dari n unsur yang berbeda.
   
   
   
2. Permutasi dengan beberapa unsur yang sama yaitu banyaknya cara untuk menyusun unsur a dan b dari n unsur yang tersedia.
   
   
   
   
3. Permutasi Siklik adalah cara menyusun n unsur yang susunannya membentuk lingkaran.
   
   
   

Kombinasi

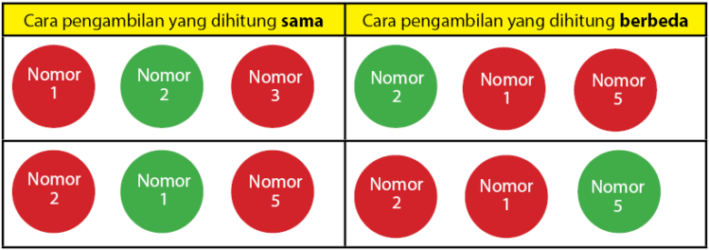
Kombinasi adalah susunan yang tidak memperhatikan urutan. Contoh permasalahan yang menggunakan kombinasi adalah mengetahui banyaknya cara untuk mengambil 3 bola dari 5 bola merah dan 2 bola hijau yang tersedia dalam sebuah kotak. Cara pengambilan bola tersebut tersebut bola merah, merah, dan kuning. Cara pengambilan lain yang mungkin adalah merah, kuning merah, dan lain sebagainya. Misalkan bola warna merah tersebut diberi nomor satu sampai dengan lima dan bola kuning juga diberi nomor satu sampai dua. Cara pengambilan bola pertama berwarna merah dengan nomor dua akan sama dengan terambilnya bola warna merah dengan nomor satu. Begitu pula dengan bola dengan warna dan nomor yang berlainan. Untuk menambah pemahaman sobat idschool, perhatikan penjelasan melalui gambar di bawah.




Mendapatkan jumlah banyaknya cara menyusun k objek dari n objek yang tersedia akan menghabiskan banyak waktu dan tidak efektif. Dalam ilmu peluang, ada sebuah rumus yang dapat digunakan untnuk menyusun k objek dari n objek yang tersedia. Cara tersebut adalah menggunakan rumus kombinasi. Banyaknya kombinasi k unsur yang diambil dari n unsur yang tersedia dinyatakan dalam rumus kombinasi di bawah.

Perbedaan Masalah Permutasi dan Kombinasi

Setelah mengetahui dua rumus tentang permutasi dan kombinasi, hal yang tidak kalah penting adalah membedakan permasalahan yang termasuk dalam permutasi atau kombinasi. Permasalahan yang sering muncul berupa soal cerita dan kita dituntut agar bisa membedakan masalah tersebut termasuk dalam permutasi atau kombinasi. Sehingga, tidak terjadi kesalahan dalam menggunakan rumus untuk menyelesaikan masalah tersebut. Perhatikan dua contoh kasus berikut.

Kasus pertama: permasalahan permutasi

Susunan panitia yang terdiri atas ketua, wakil ketua, sekretaris, dan bendahara akan dibentuk untuk mensukseskan suebuah acara. Susunan panitia tersebut akan dipilih dari 10 orang terpilih berdasarkan kriteria yang telah ditentukan. Berapakah banyaknya susunan panitia yang dapat dibentuk?

Kasus ke dua: permasalahan kombinasi

Enam buku akan dipilih dari lima buku Matematika, tiga buku Fisika, dan empat buku Kimia untuk disumbangkan ke sekolah untuk anak jalanan. Berapakah banyaknya cara yang dapat dilakukan untuk memilih enam buku tersebut?

Pada kasus pertama, susunan urutan menjadi bagian yang perlu diperhatikan. Kedudukan ketua untuk orang pertama tentu akan berbeda dengan ketua yang ditempati oleh orang ke tiga. Begitu juga dengan kududukan untuk posisi lainnya. Sedangkan pada contoh kasus kedua, pemilihan buku pada urutan pertama dan kedua misalnya adalah buku Matematika pertama dan buku Matematika ke dua, keduanya merupakan buku Matematika. Sehingga, urutan tidak dipehatikan. Intinya, rumus permutasi digunakan untuk permasalahan yang memperhatikan urutan. Sedangkan kombinasi digunakan untuk menyelesaikan permasalahan yang tidak memperhatikan urutan.